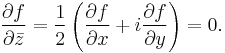Looman–Menchoff theorem
In the mathematical field of complex analysis, the Looman–Menchoff theorem states that a continuous complex-valued function defined in an open set of the complex plane is holomorphic if and only if it satisfies the Cauchy–Riemann equations. It is thus a generalization of a theorem by Goursat, which instead of assuming the continuity of f, assumes its Fréchet differentiability when regarded as a function from a subset of R2 to R2.
A complete statement of the theorem is as follows:
- Let Ω be an open set in C and f : Ω → C a continuous function. Suppose that the partial derivatives
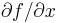and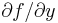 
exist everywhere but a countable set in Ω. Then f is holomorphic if and only if it satisfies the Cauchy–Riemann equation:
References
- Gray, J. D.; Morris, S. A. (1978), "When is a Function that Satisfies the Cauchy-Riemann Equations Analytic?", The American Mathematical Monthly 85 (4): 246–256, April 1978, doi:10.2307/2321164, JSTOR 2321164.
- Looman, H. (1923), "Über die Cauchy–Riemannschen Differentialgleichungen", Göttinger Nach.: 97–108.
- Menchoff, D. (1936), Les conditions de monogénéité, Paris.
- Montel, P. (1913), "Sur les différentielles totales et les fonctions monogènes", C. R. Acad. Sci. Paris 156: 1820–1822.
- Narasimhan, Raghavan (2001), Complex Analysis in One Variable, Birkhäuser, ISBN 0817641645, http://books.google.com/?id=J-J4HmIDnOwC&pg=PA43&lpg=PA43&dq=%22Looman-Menchoff+theorem%22.